Clique para aprender o que são posições relativas entre circunferências e descubra a diferença entre disjuntas, secantes e tangentes.
Quando duas circunferências são definidas em um mesmo plano, podemos analisar as posições que uma delas ocupa com relação à outra. Assim, as posições relativas entre duas circunferências são: disjuntas, tangentes e secantes.
Circunferências disjuntas
Duas circunferências são chamadas de disjuntas quando não possuem pontos em comum. Existem dois casos a considerar a respeito dessa posição relativa entre as circunferências:
1 – Circunferências disjuntas externas
Duas circunferências são disjuntas externas quando não possuem nenhum ponto em comum e, ao mesmo tempo, quando uma delas está na região externa da outra. A figura a seguir mostra exemplos circunferências disjuntas externas.
A distância entre os centros das circunferências disjuntas externas sempre será maior que a soma de seus raios. Caso essa distância seja igual ou inferior à soma dos raios, as circunferências passam a ter pontos em comum.
2 – Circunferências disjuntas internas
Duas circunferências são disjuntas internas quando não possuem pontos em comum e, ao mesmo tempo, quando uma está na região interna da outra, como mostra a figura a seguir.
A diferença entre os raios dessas circunferências sempre será maior que a distância entre os centros das duas.
Circunferências tangentes
Duas circunferências são chamadas de tangentes quando possuem um único ponto em comum. As circunferências tangentes também podem ser classificadas como internas ou externas.
1 – Duas circunferências são tangentes externas quando possuem um único ponto em comum e, além disso, uma delas está na região externa da outra.
2 – Duas circunferências são tangentes internas quando possuem um único ponto em comum e, além disso, uma delas está na região interna da outra.
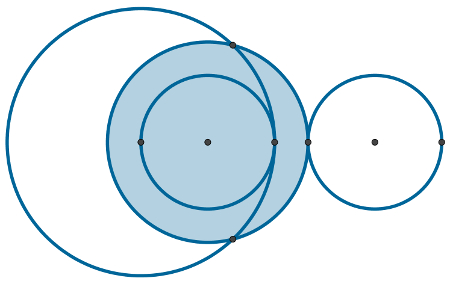
A imagem a seguir mostra exemplos de circunferências tangentes internas e tangentes externas.
Observe que as circunferências tangentes externas possuem a seguinte característica: a soma de seus raios é igual à distância entre seus centros. Nas tangentes internas, a diferença entre seus raios é igual à distância entre seus centros.
Circunferências secantes
Duas circunferências são chamadas de secantes quando possuem apenas dois pontos em comum.