O volume do cone é calculado ao multiplicarmos a área da base pela altura e dividirmos o resultado por três. Como a base do cone é um círculo, sua área depende do raio.

O volume do cone é calculado quando multiplicamos a área da base e a altura e dividimos por três. Esse é um dos cálculos que podem ser feitos em relação a esse sólido geométrico, classificado como corpo redondo por ser formado por uma base circular ou por ser constituído por meio da rotação de um triângulo.
Leia também: Quais são as medidas de volume?
Para calcular o volume do cone, é necessário conhecer as medidas do raio da base e da altura.
O volume do cone é calculado pela fórmula:
\(V=\frac{\pi r^2\cdot h}{3}\)
Como a base do cone é um círculo, utilizamos a fórmula da área do círculo para calcular a área da base do cone, ou seja, \(A_b=\pi r^2\).
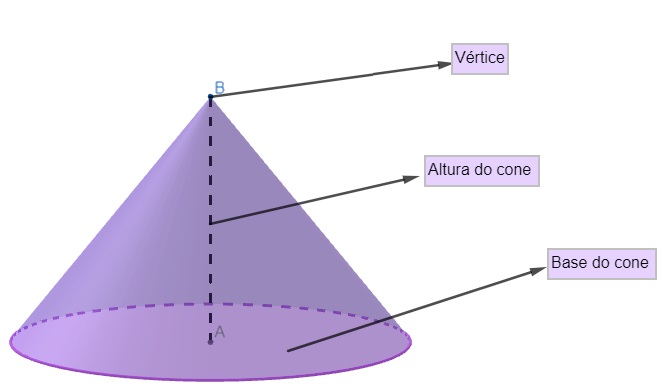
O cone é conhecido como corpo redondo ou sólido de revolução pelo fato de ele possuir uma base formada por um círculo. Esse sólido geométrico é bastante comum no nosso dia a dia, utilizado, por exemplo, no trânsito para sinalizar uma área em que os carros não podem passar. O cone possui três elementos importantes: a altura, a base e o vértice.
O volume de um cone é calculado pelo produto entre a área da base e a altura dividido por três, ou seja, ele pode ser calculado pela fórmula:
\(V=\frac{A_b\cdot h}{3}\)
V: volume
Ab: área da base
h: altura do cone
Acontece que nem sempre a área da base é conhecida. Nesse caso, como a base de um cone é formada por um círculo, podemos utilizar a fórmula da área do círculo para calcular a área da base. Ou seja, em um cone a área da base é calculada por \(A_b=\pi r^2\), o que nos permite calcular seu volume utilizando a fórmula:
\(V=\frac{\pi r^2\cdot h}{3}\)
V: volume do cone
r: raio da base
h: altura do cone
Para calcularmos o volume do cone, é necessário encontrar os valores da sua altura e do seu raio. Conhecendo esses dados, basta substituir os valores na fórmula do volume do cone e realizar os cálculos necessários.
Exemplo 1:
Calcule o volume do cone que possui raio medindo 5 cm e altura medindo 12 cm.
Resolução:
Sabemos que:
r = 5 cm
h = 12 cm
Substituindo na fórmula:
\(V=\frac{\pi r^2\cdot h}{3}\)
\(V=\frac{\pi\cdot5^2\cdot12}{3}\)
\(V=\frac{\pi\cdot25\cdot12}{3}\)
\(V=\frac{300\pi}{3}\)
\(V=100\pi cm^3\)
Exemplo 2:
Calcule o volume do cone a seguir, utilizando 3,1 como aproximação para o valor de π.
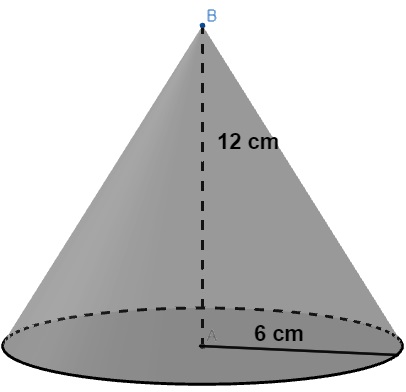
Resolução:
Os dados são:
r = 6 cm
h = 12 cm
π = 3,1
Calculando o volume do cone:
\(V=\frac{\pi r^2\cdot h}{3}\)
\(V=\frac{3,1\cdot6^2\cdot12}{3}\)
Veja também: Como se calcula o volume do cilindro?
Questão 1
Um reservatório foi construído no formato de um cone. Sabendo que ele possui diâmetro da base medindo 8 metros e altura igual a 5 metros, sendo π = 3, o volume desse reservatório é de:
A) 12 m³
B) 15 m³
C) 18 m³
D) 20 m³
E) 22 m³
Resolução:
Alternativa D.
Considerando que o diâmetro da base é de 8 metros e que o raio é metade do diâmetro:
r = 8 : 2 = 4 m
As outras informações são que h = 5 e π = 3.
Calculando o volume do cone:
\(V=\frac{\pi r\cdot h}{3}\)
\(V=\frac{3\cdot4\cdot5}{3}\)
\(V=4\cdot5\)
\(V=20\ m^3\)
Questão 2
Uma embalagem no formato de cone deve ter 310 m³. Sendo a altura dessa embalagem de 12 cm, seu raio deve ser de: (Utilize 3,1 como aproximação de π)
A) 3 cm
B) 4 cm
C) 5 cm
D) 6 cm
E) 7 cm
Resolução:
Alternativa C
Os dados são que V = 310, h = 12 e π = 3,1.
Substituindo os valores conhecidos na fórmula do volume:
\(V=\frac{\pi r^2\cdot h}{3}\)
\(310=\frac{3,1\cdot r^2\cdot12}{3}\)
\(310\cdot3=3,1\cdot r^2\cdot12\)
\(930=37,2r^2\)
\(\frac{930}{37,2}=r^2\)
\(25=r^2\)
\(r=\sqrt{25}\)
\(r=5\ cm\)
Portanto, o raio deve ser de 5 cm.