Volume do cilindro

O volume do cilindro é calculado pela multiplicação entre a área da base e a altura. Como a base é um círculo, utilizamos a fórmula da área de um círculo vezes a altura desse cilindro. O cilindro é uma figura geométrica formada por duas bases circulares e área lateral que liga esses dois círculos.

Essa forma é bastante comum no dia a dia, vista em latas de refrigerante e cilindros de oxigênio, entre outros objetos. Calcular o volume do cilindro é calcular o espaço que ele ocupa e também a sua capacidade, por exemplo, para saber a quantidade de ml que tem na lata de refrigerante.

O cilindro é um objeto bastante comum também em laboratórios para experimentos químicos em que o volume é de grande importância, por exemplo, para calcular a densidade de um objeto, precisamos do seu volume.

Leia também: Cone – sólido geométrico que também possui um círculo como sua base

Fórmula do volume do cilindro

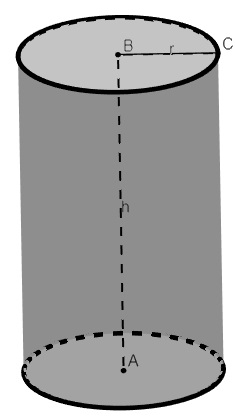
Para saber o volume de um cilindro, precisamos calcular o produto entre a área da base A_b e a altura h dele, porém, ao analisarmos a figura, sabemos que sua base é um círculo. A área de um círculo de raio r é calculada pela fórmula A_círculo = π r², o que justifica a fórmula para calcular-se o volume do cilindro:

h → altura
r → raio da base

Como calcular o volume do cilindro?

Para que seja possível aplicar a fórmula, precisamos do valor da altura e do raio do cilindro, então realizamos as substituições do valor do raio e da altura e, quando necessário, utilizamos uma aproximação do valor de π.

Exemplo 1:

Calcule o volume do cilindro a seguir (use π = 3,1):

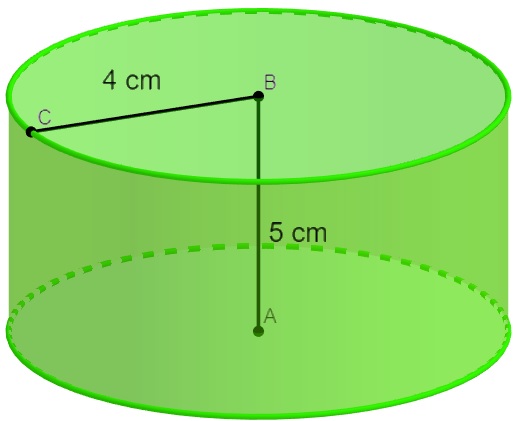
Para calcular o volume, temos que r = 4 e h = 5, então, realizando as substituições, temos que:

V = π · r² · h

V = 3,1 · 4² · 5

V = 3,1 · 16 · 5

V = 3,1 · 80 = 248 cm³

Veja também: Como calcular a área total do cilindro?

Exercícios resolvidos

Questão 1 - Marta está fazendo a reforma da sua casa e decidiu trocar a caixa d’água. Essa nova caixa d’água tem formato cilíndrico. Sabendo que as dimensões da caixa escolhida é de 1,20 metro de diâmetro e 5,40 metros de altura, e sabendo que, após 12 horas, ela estará com metade do seu volume preenchido, qual será a quantidade, em litros, de água que haverá na caixa nesse momento? (Dica: 1 m³ = 1000 litros e use π = 3.)

a) 8748

b) 2916

c) 23328

d) 11664

e) 5832

Resolução

Alternativa B

Como o diâmetro d = 1,20, sabemos que o raio é a metade do diâmetro, ou seja, r = 0,60 metro. 

V = π · r² · h

V = 3 · 0,6² · 5,4

V = 3 · 0,36 · 5,4

V = 5,832 m³

Multiplicando por 1000, para converter em litros, temos que:

5,832 · 1000 = 5832 litros

Esse é o volume total, como queremos a metade, basta realizar a divisão de 5832 por 2. 

5832 : 2= 2916 litros

Questão 2 - Um caminhão de transporte de combustível possui um reservatório no formato de um cilindro conforme a imagem a seguir:

Ao analisar-se o cilindro do reservatório, constatou-se que o raio do reservatório é igual a 2 metros, lembrando-se de que em 1 m³ cabem 1000 litros, qual deve ser o valor mínimo da altura desse cilindro para que o caminhão consiga transportar 54 mil litros de combustível? (Use π = 3.)

a) 5 metros

b) 4,5 metros

c) 9 metros

d) 3,5 metros

e) 7 metros

Resolução

Alternativa B

Sabemos que o volume V tem que ser igual a 54 000 litros e que cada 1 m³ = 1000 litros, logo, o reservatório precisa ter 54 m³.

Então:

V = 54 m³

π · r² · h = 54

Dados π = 3 e r = 2, então:

3 · 2² · h = 54

3 · 4 · h = 54

12 · h = 54

h = 54 : 12

h = 4,5 metros