Quadrado é uma figura plana que tem 4 lados, todos com a mesma medida. Ele é bastante comum no cotidiano, sendo presente, por exemplo, no formato de algumas paredes.

O quadrado é uma figura plana, classificado como polígono, composto por 4 lados e 4 ângulos congruentes entre si, ou seja, que possuem as mesmas medidas. O quadrado é uma figura geométrica bastante comum no cotidiano e é um caso especial de quadrilátero estudado pela geometria plana.
Saiba mais: Geometria analítica — área que estuda a Geometria utilizando ferramentas algébricas
É um polígono que possui 4 lados e 4 ângulos com a mesma medida.
Para calcular sua área, utilizamos a fórmula \(A=l^2\).
Para calcular seu perímetro, utilizamos a fórmula \(P=4l\).
Para calcular sua diagonal, utilizamos a fórmula \(d=l\sqrt2\).
É um caso particular de retângulo e de losango.
O quadrado é um polígono que possui 4 lados e 4 ângulos congruentes entre si, ou seja, os seus 4 lados e os seus 4 ângulos têm a mesma medida. O quadrado é uma forma geométrica bastante presente no cotidiano, como no formato da maioria dos pisos, na superfície de algumas mesas, entre outros objetos.
O quadrado é um entre vários tipos de quadriláteros, estudados na geometria plana, e é uma forma geométrica bastante comum na construção civil.
Assim como nos demais polígonos, como principais elementos do quadrado, podemos destacar seus vértices, seus lados, suas diagonais e seus ângulos.
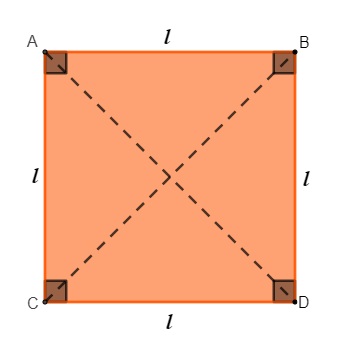
Vértices: os pontos A, B, C e D são os vértices do quadrado.
Lados: os segmentos \(\overline{AB},\overline{AC},\overline{BD}\ e\ \overline{CD}\) são os lados do quadrado.
Diagonal: os segmentos AD e BC são as diagonais do quadrado.
Ângulos: podemos perceber a presença de 4 ângulos internos, e todos com 90°, são eles: \(CÂB,BCD,CDB e ABD\).
O quadrado possui propriedades importantes herdadas pelo fato de ele ser um quadrilátero e também por ser classificado como paralelogramo, além disso, é um caso especial de retângulo, pois todos os seus ângulos medem 90°, e losango, pois todos os lados têm a mesma medida, ou seja, são congruentes.
As principais características do quadrado são:
A soma dos ângulos internos de um quadrilátero é de 360°.
Os ângulos internos medem 90° cada, logo, ele possui 4 ângulos retos.
Os lados são congruentes.
As diagonais são congruentes.
As diagonais se interceptam em seus pontos médios.
As diagonais são perpendiculares entre si.
Veja também: Poliedros — os sólidos geométricos que têm faces formadas por polígonos
Para calcular a área do quadrado, realizamos a multiplicação da sua base pela sua altura, como a base e a altura têm a mesma medida, então a área do quadrado é calculada pela fórmula:
\(A=l^2\)
Exemplo:
Um quadrado tem lado medindo 15 cm, então, qual é o valor da sua a área?
Resolução:
Substituindo l por 15 cm na fórmula, temos que:
\(A=l^2\)
\(A={15}^2\)
\(A=225\ cm²\)
O perímetro do quadrado é igual à soma do comprimento dos seus lados, como os lados são todos congruentes, temos que:
\(P=4l\)
Exemplo:
Calcule o perímetro de um quadrado que possui lados medindo 15 cm.
Resolução:
Sabemos que \(P=4l\), substituindo l = 15, temos que:
\(P=4l\ \)
\(P=4\cdot15\ \)
\(P=60\ cm\ \)
Então o perímetro desse quadrado é de 60 cm.
O quadrado possui duas diagonais, sendo que ambas têm a mesma medida de comprimento. Quando traçamos uma diagonal do quadrado, é possível perceber que ela o divide em dois triângulos retângulos:
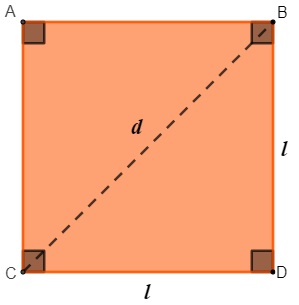
Para calcular o comprimento da diagonal, podemos fazer a aplicação do teorema de Pitágoras no triângulo CDB, que tem como hipotenusa a diagonal do retângulo, logo, temos que:
\(d^2=l^2+l^2\)
\(d^2=2l^2\)
\(d=\sqrt{2l^2}\)
\(d=l\sqrt2\)
Assim, a diagonal do quadrado é igual ao produto do comprimento do lado do quadrado por \(\sqrt2\).
Exemplo:
Qual é o comprimento da diagonal de um quadrado que tem lado medindo 9 cm de comprimento?
Resolução:
Para calcular o comprimento da diagonal, basta multiplicar o lado por \(\sqrt2\).
Então temos que:
\(d=l\sqrt2\)
\(d=9\sqrt2\ cm\)
Como não temos uma aproximação para o valor de \(\sqrt2\), deixamos a diagonal como \(9\sqrt2\ cm\). Em alguns casos, quando essa informação é dada, podemos substituir \(\sqrt2\) pela sua aproximação, a fim de encontrar o valor aproximado do comprimento da diagonal.
Exemplo 2:
Se um quadrado tiver lados medindo 5 cm, e utilizando 1,4 como aproximação para \(\sqrt2\), qual será o comprimento da diagonal desse quadrado?
Resolução:
Calculando o comprimento da diagonal, temos que:
\(d=l\sqrt2\)
\(d=5\sqrt2\)
\(d=5\cdot1,4\)
\(d=7,0\ cm\)
Leia também: Soma dos ângulos internos de um polígono — a expressão matemática que pode ser usada nesse cálculo
Questão 1
Parte de um terreno tem formato de quadrado com lados medindo 6 metros cada, e sabe-se que um agricultor deseja plantar soja nele. Para fazer a plantação de soja, a máquina semeadora joga 13 sementes em cada metro quadrado. Então a quantidade de sementes necessárias para cultivar soja nesse terreno será igual a:
A) 390 sementes
B) 468 sementes
C) 529 sementes
D) 652 sementes
Resolução:
Alternativa B
Primeiro calcularemos a área do terreno, como ele é um quadrado, temos que:
\(A=l^2\)
\(A=6^2\)
\(A=36\ m^2\)
Como ele tem 36 m², então, para calcular a quantidade de sementes necessárias Q, basta multiplicar 13 por 36.
\(Q=36\cdot13\)
\(Q=468\ sementes\)
Questão 2
Um quadro, no formato de um quadrado com 22 cm de lado, será moldurado. Supondo que essa moldura tenha o tamanho exato do perímetro do quadrado, então o seu comprimento será igual a:
A) 88 cm
B) 92 cm
C) 100 cm
D) 102 cm
Resolução:
Alternativa A
Calculando o perímetro do quadrado, temos que:
\(P=4l\)
\(P=4\cdot22\)
\(P=88\ cm\)