O triângulo isósceles possui como principal característica dois lados congruentes, ou seja, possui dois lados iguais. Isso implica a presença de dois ângulos internos congruentes, e eles recebem o nome de ângulos da base. Por ser uma figura plana, vamos determinar uma expressão que nos possibilite calcular sua área.
Leia também: Qual é a condição de existência de um triângulo?
Considere o triângulo isósceles ABC.
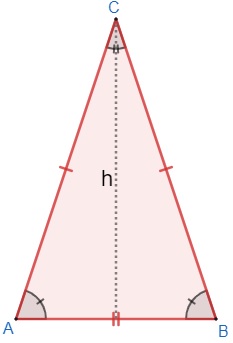
No triângulo, veja que os lados AC e BC são congruentes. O ângulo oposto a esses lados, AB, é incongruente e chamado de ângulo da base ou base do triângulo retângulo.
Uma outra importante propriedade dos triângulos isósceles é a coincidência da altura e da mediana relativas à base do triângulo, ou seja, o segmento de reta perpendicular à base do triângulo e o segmento de reta que divide essa base são iguais.
Observe que esse segmento de reta divide o triângulo isósceles exatamente ao meio, por esse fato, esse segmento é também chamado de eixo de simetria.
Leia também: Classificação dos triângulos – critérios e nomes
Área do triângulo isósceles
Sabe-se que a área de qualquer triângulo é dada pela seguinte fórmula:
![]()
De modo geral, em problemas de cálculo de área de triângulos isósceles, basta encontrarmos a altura utilizando o teorema de Pitágoras.
Para encontrarmos a área de um triângulo isósceles, vamos considerar o seguinte exemplo.
Determine a área do triângulo a seguir:
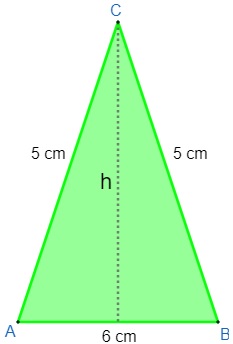
Observe que o triângulo ABC é isósceles, pois possui dois lados iguais. Veja também que a altura dividiu o triângulo isósceles em dois. Assim sendo, vamos encontrar a altura e substituir na fórmula. Lembre-se de que a altura coincide com a mediana, ou seja, ela divide o lado AB ao meio.
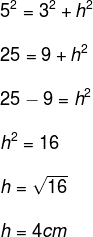
Substituindo o valor da altura na fórmula, temos:
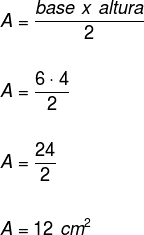

Questão 1 – Sabe-se que, em um triângulo isósceles, o ângulo interno oposto à base mede 30°. Determine a medida dos ângulos da base.
Resolução
Vamos construir um triângulo isósceles para facilitar a resolução, lembre-se de que os ângulos da base são iguais, logo, podemos representá-los com a mesma letra.
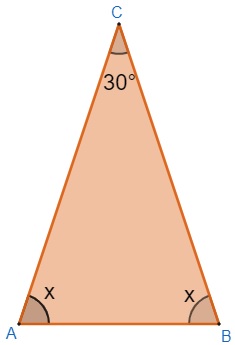
Sabemos também que a soma dos ângulos internos de um triângulo é 180°, logo:
x + x + 30° = 180°
2x = 180° – 30°
2x = 150°
x = 150° ÷ 2
x = 75°