O trapézio é um caso particular de quadrilátero, composto por dois lados paralelos, conhecidos como base, e dois lados não paralelos, conhecidos como lados oblíquos.

O trapézio é um quadrilátero que possui dois lados paralelos e dois lados não paralelos. Os lados paralelos do trapézio são conhecidos como base maior e base menor. Já os lados não paralelos são chamados de lados oblíquos. Existem três tipos diferentes de trapézio: o trapézio isósceles, o trapézio retângulo e o trapézio escaleno.
Leia também: Quais são as formas geométricas?
\(A=\frac{\left(B+b\right)\cdot h}{2}\)
O trapézio é um quadrilátero. Ele possui dois lados paralelos e dois lados não paralelos. Veja um exemplo de trapézio e os seus principais elementos:
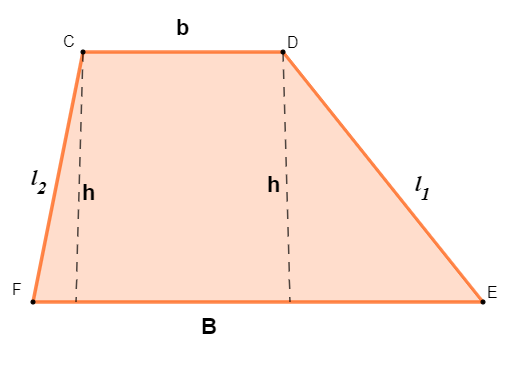
Além dos elementos destacados na imagem, sabemos que a o trapézio possui 4 ângulos internos. Como ele é um quadrilátero, a soma dos ângulos internos é igual a 360°.
Existem três classificações possíveis para um trapézio. O trapézio pode ser isósceles, retângulo ou escaleno.
O trapézio isósceles é o trapézio que possui os lados oblíquos congruentes:

É o trapézio que possui um dos lados oblíquo, perpendicular às bases do trapézio, ou seja, um lado oblíquo faz um ângulo de 90° com as bases do trapézio.

O trapézio é escaleno se a medida dos lados são todas distintas.

Existem propriedades específicas para os trapézios. Veja cada uma delas a seguir.

w + x = 180°
y + z = 180°

Para calcular o perímetro de um trapézio, basta calcular a soma dos seus lados, como no exemplo a seguir.
Exemplo:
Calcule o perímetro deste trapézio:
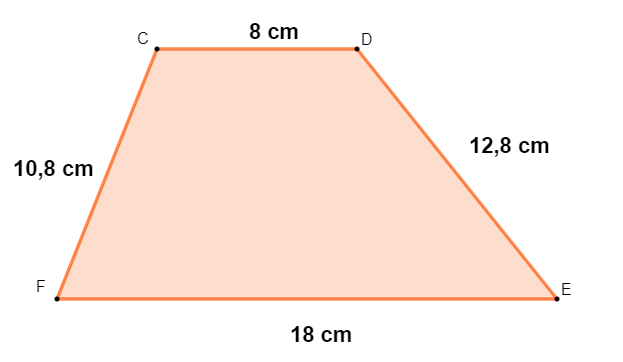
Resolução:
\(P=10,8+8+12,8+18\ \)
\(P=49,6\ cm\)
Para calcular a área de um trapézio, utilizamos a fórmula:
\(A=\frac{\left(B+b\right)\cdot h}{2}\)
Exemplo:
Um trapézio possui 12 cm de altura e bases medindo 15 cm e 22 cm, então a área desse trapézio é igual a:
Resolução:
\(A=\frac{\left(B+b\right)\cdot h}{2}\)
\(A=\frac{\left(22+15\right)\cdot12}{2}\)
\(A=\frac{37\cdot12}{2}\)
\(A=\frac{37\cdot12}{2}\)
\(A=\frac{444}{2}\)
\(A=222\ cm^2\)
Leia também: Polígonos — figuras geométricas formadas por segmentos de reta
Questão 1
Parte de um terreno possui formato de um trapézio, com bases medindo 9 metros e 13 metros. Se a altura dessa região é de 5 metros, então a sua área mede:
A) 40 m²
B) 45 m²
C) 50 m²
D) 55 m²
Resolução:
Alternativa D
Calculando a área do terreno, temos que:
\(A=\frac{\left(13+9\right)\cdot5}{2}\)
\(A=\frac{22\cdot5}{2}\)
\(A=\frac{110}{2}\)
\(A=55{\ m}^2\)
Questão 2
Sobre o trapézio, podemos afirmar que:
I – lados opostos do trapézio são sempre paralelos.
II – o trapézio é um quadrilátero.
III – o trapézio possui duas bases, uma base maior e uma base menor.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas são afirmativas são verdadeiras.
Resolução:
Alternativa A
A afirmativa I é falsa, pois o trapézio possui somente dois lados paralelos entre si. Os outros dois não são.
As demais afirmativas são verdadeiras, pois o trapézio é um quadrilátero e ele possui uma base maior e uma base menor.