Propriedades da potenciação

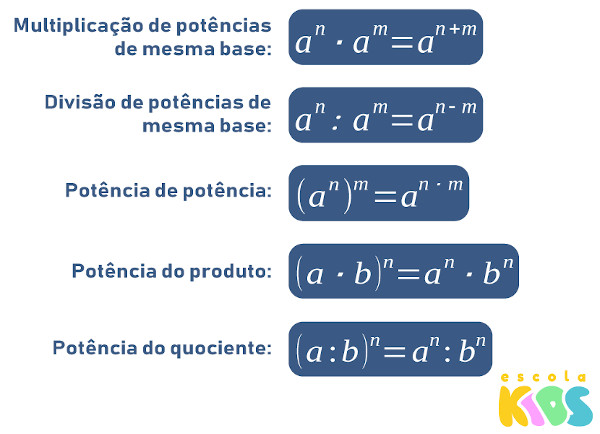
As propriedades da potenciação são técnicas que utilizamos para facilitar a resolução de cálculos envolvendo potências. São elas: multiplicação de potência de mesma base, divisão de potência de mesma base, potência de potência, potência do produto e potência do quociente. Além dessas propriedades, existem também três casos particulares de potência que devem ser considerados: base da potência igual a 1, expoente da potência igual a 1 e expoente da potência igual a 0.

Veja também: Propriedades da multiplicação para cálculo mental

Videoaula sobre propriedades da potência

Potenciação

Antes de falar sobre as propriedades da potenciação, é importante relembrarmos o que é a potenciação.  A potenciação é a operação matemática que representa a multiplicação sucessiva de um número por ele mesmo. Quando representados \(a^n\) (lê-se: a elevado a n), estamos realizando a multiplicação sucessiva de a por ele mesmo n vezes.

• Exemplos:

5³ = 5 ⋅ 5 ⋅ 5 = 125

24 = 2 ⋅ 2 ⋅ 2 ⋅ 2 = 16

A potenciação é uma operação com muitas aplicabilidades. Com os estudos dessa operação foi possível desenvolver algumas propriedades que facilitam as contas.

Propriedades da potenciação

Propriedades da potenciação são técnicas que podemos aplicar para facilitar o cálculo de casos particulares de operações envolvendo potência. Veremos cada uma delas a seguir.

→ Multiplicação de potências de mesma base

Na multiplicação de potência de mesma base, conservamos a base e somamos os expoentes:

\(a^n⋅a^m=a^{n+m}\)

Exemplos:

\(3^2⋅3^4=3^{2+4}=3^6\)

\(5^3⋅5^9=5^{3+9}=5^{12}\)

→ Divisão de potências de mesma base

Quando há uma divisão de potências de mesma base, conservamos a base e subtraímos os expoentes.

\(a^n:a^m=a^{n-m}\)

Exemplos:

\(3^6:3^4=3^{6-4}=3^2\)

\(5^7:5^3=5^{7-3}=5^4\)

→ Potência de potência

Na potência de potência, conservamos a base e multiplicamos os expoentes.

\((a^n)^m=a^{n⋅m}\)

Exemplos:

\((3²)^5=3^{2⋅5}=3^{10}\)

\((5^3)^4=5^{3⋅4}=5^{12}\)

→ Potência do produto

Quando a base da potência é um produto, podemos calcular o produto entre cada uma das parcelas elevadas a potências.

\((a⋅b)^n=a^n⋅b^n\)

Exemplos:

\((4⋅5)^2=4^2⋅5^2\)

\((2⋅4)^3=2^3⋅4^3\)

→ Potência do quociente

Quando a base da potência é um quociente, podemos calcular a divisão entre as potências.

\((a:b)^n=a^n:b^n\)

Exemplos:

\((15∶9)^6=15^6:9^6\)

\((8∶5)^3=8^3:5^3\)

Casos particulares de potenciação

Além das propriedades da potenciação, existem alguns casos particulares. Veja a seguir.

→ Base da potência igual a 1

Quando a base da potência é 1, 1 elevado a qualquer expoente será igual a 1.

Exemplos:

\(1^{10}=1\)

\(1^{12321}=1\)

→ Expoente da potência igual a 1

Quando o expoente da potência é 1, temos que todo número elevado a 1 é igual a ele mesmo.

Exemplos:

\(123^1=123\)

\(5290^1=5290\)

→ Expoente da potência igual a 0

Quando o expoente da potência é 0, temos que todo número elevado a 0 é igual a 1.

Exemplos:

\(500^0=1\)

\(3012^0=1\)

Saiba mais: Raiz quadrada — um caso particular da operação inversa da potenciação

Exercícios resolvidos sobre propriedades da potenciação

Questão 1

Simplificando a expressão

\(\frac{2^4⋅4^3⋅8^{10}}{32^6} \)

encontramos:

A) 2⁸

B) 2¹⁰

C) 2¹⁵

D) 2²⁰

E) 2³⁰

Resolução:

Alternativa B

Primeiramente, escreveremos todas as potências como potência de base 2.

Sabemos que 4 = 2², logo temos que 4³ = (2²)³. Utilizando a propriedade de potência, temos que:

\((2^2 )^3=2^{2⋅3}=2^6\)

Sabemos que 8 = 2³, então:

\(8^{10}=(2^3 )^{10}=2^{30}\)

Temos que 32 = 2⁵:

\(32^6=(2^5 )^6=2^{5⋅6}=2^{30}\)

Portanto:

\(\frac{2^4⋅4^3⋅8^{10}}{32^6} =\frac{2^4⋅2^6⋅2^{30}}{2^{30}}\)

\(\frac{2^4⋅4^3⋅8^{10}}{32^6}=\frac{2^{4+6+30}}{2^{30}} \)

\(\frac{2^4⋅4^3⋅8^{10}}{32^6}=\frac{2^{40}}{2^{30}} \)

\(\frac{2^4⋅4^3⋅8^{10}}{32^6} =2^{40-30}\)

\(\frac{2^4⋅4^3⋅8^{10}}{32^6} =2^{10}\)

Questão 2

Analise as afirmativas a seguir e julgue cada uma como verdadeira ou falsa.

I) \(2^5+2^8=2^{13}\)

II) \(2^{12} ∶ 2^8=2^4\)

III) \((2^4 )^3=2^{12}\)

Marque a alternativa correta:

A) Somente I é falsa.

B) Somente II é falsa.

C) Somente III é falsa.

D) Todas são verdadeiras.

Resolução:

Alternativa A

Podemos perceber que a afirmativa I é falsa, pois somente na multiplicação de potência de mesma base é que podemos conservar as bases e somar os expoentes. Note que não temos uma multiplicação, mas sim uma adição. As demais afirmativas são verdadeiras, pois mostram, respectivamente, a propriedade da divisão de potência de mesma base e a propriedade da potência de potência.