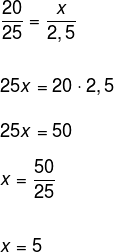A proporção consiste na igualdade entre duas ou mais razões, que são a divisão entre números na qual devemos obedecer a ordem em que eles são colocados. Por exemplo, na sequência de Fibonacci, a razão entre qualquer termo e o seu antecessor será sempre proporcional, ou seja, igual. O estudo das proporções é de muita importância, uma vez que, na natureza e em nosso cotidiano, esse conceito aparece frequentemente.
Leia também: Regra de três: como calcular?
Para melhor entendermos a definição de proporção, antes é necessário saber o que é uma razão. Uma razão nada mais é que o quociente entre os números envolvidos na operação, veja:
Seja a e b dois números quaisquer, com b ≠ 0, a sua razão é dada pela divisão entre ambos:
![]()
Determine as razões entre 2 e 3; 7 e 9; 4 e 18. Para isso, devemos escrever as frações (divisões) entre os números em questão na ordem que foram colocados.
![]()
Quando igualamos duas razões, estamos estabelecendo uma proporção.
Sejam os números a, b, c e d, com b ≠ 0 e d ≠ 0, a razão entre eles, nessa ordem, forma uma proporção, ou seja:
![]()
Se a igualdade for verdadeira, isto é, se a · d = b · c, então os números a, b, c e d são proporcionais.
Verifique se os números a seguir são proporcionais ou não.
a) 2, 4, 8 e 16
Para que esses números sejam proporcionais, as razões entre eles devem ser iguais, vamos verificar.
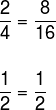
Veja que, após montar as razões, simplificamos as frações e obtemos duas destas, logo, os números são proporcionais. Outra maneira de verificar se eles são proporcionais é realizando a multiplicação cruzada, veja:
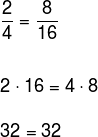
Após a multiplicação cruzada, se a igualdade for verdadeira, os números são proporcionais. Você pode escolher qual método achar melhor para a verificação, no exemplo a seguir, vamos utilizar somente a multiplicação cruzada, veja:
b) 3, 5, 2, 3
Montamos as razões e, em seguida, realizamos a multiplicação cruzada.
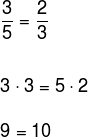
Veja que a igualdade não é verdadeira, logo, os números não são proporcionais.
Leia também: Simplificação de frações: o que é e como fazer?
Conhecendo as definições de razão e proporção, podemos agora entender a diferença entre elas. A razão é a divisão entre dois números conhecidos, e a proporção é a igualdade entre esses números.
A proporção possui algumas propriedades que podem facilitar na resolução de alguns problemas, entretanto, as duas primeiras merecem uma atenção especial. Veja, a seguir, quais são.
Propriedade 1 - Considere a proporção:
![]()
Então a próxima igualdade é verdadeira:
![]()
Propriedade 2 - Também conhecida como propriedade fundamental das proporções.
![]()
Para todas as propriedades seguintes, considere a definição de proporção.
Propriedade 3 - A razão entre a e c é igual à razão entre a + c e b + d.
![]()
Propriedade 4 - Dada a definição de proporção, então a igualdade seguinte é verdadeira.
![]()
Questão 1 - (Unicamp - SP) A razão entre a idade de Pedro e a de seu pai é igual a dois nonos. Se a soma das duas idades é igual a 55 anos, então Pedro tem:
a) 12 anos
b) 13 anos
c) 10 anos
d) 15 anos
Solução
Alternativa c.
Como não sabemos as idades de Pedro e de seu pai, vamos chamá-las de x e y, respectivamente.
x → idade de Pedro
y → idade do pai
A razão entre a idade de Pedro e a de seu pai é igual a dois nonos, veja que temos uma igualdade entre razões, logo, uma proporção.
![]()
De acordo com o enunciado, temos que a soma das idades é de 55, logo:
x + y = 55
Agora, utilizando a propriedade 4 da proporção, temos:

Questão 2 - Sabe-se que os números 20, 25, x e 2,5 são proporcionais nessa ordem. Determine o valor de x com base nessas informações.
Solução
Como os números são proporcionais em determinada ordem, então temos a seguinte proporção (após montá-la, utilizamos a propriedade 2):