Clique e aprenda a calcular cinco produtos notáveis mais importantes para a álgebra e descubra uma técnica para encontrá-los facilmente.
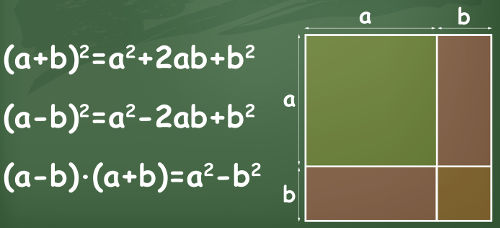
Produtos notáveis são as cinco multiplicações mais usadas entre polinômios. Os resultados desses produtos são muito comuns e encontrados na solução de diversos problemas, tanto na forma de polinômio quanto na de equação do segundo grau. Os cinco produtos notáveis mais importantes são: quadrado da soma, quadrado da diferença, produto da soma pela diferença, cubo da soma e cubo da diferença.
Os produtos notáveis podem ser usados como fórmulas para calcular potências envolvendo polinômios. Para compreender esse uso, é necessário discutir essas “fórmulas” e o modo como elas são criadas.
Quadrado da soma
O produto notável conhecido como quadrado da soma sempre pode ser colocado na forma a seguir:
(x + a)2
Observe que elevar essa soma ao quadrado é o mesmo que calcular a seguinte multiplicação:
(x + a)(x + a)
Usando a propriedade distributiva da multiplicação sobre a adição – mais conhecida como “chuveirinho” – obtemos:
(x + a)(x + a) =
x2 + xa + ax + a2
Somando os termos semelhantes, temos:
x2 + xa + ax + a2 =
x2 + 2ax + a2
Note que, comparando esse resultado ao produto notável inicial, podemos concluir que:
O quadrado do primeiro termo,
somado a duas vezes o primeiro, vezes o segundo termo,
somado ao quadrado do segundo termo,
é igual ao quadrado da soma.
Essa é a regra que deve ser memorizada, caso queira evitar de fazer esses cálculos em todos os quadrados da soma.
Quadrado da diferença
O quadrado da diferença é semelhante ao quadrado da soma, a única diferença é que o resultado terá um sinal negativo, de acordo com os cálculos a seguir. O quadrado da diferença é o produto notável que pode ser escrito na seguinte forma:
(x – a)2
Para encontrar o resultado desse quadrado, basta escrevê-lo na forma de produto e usar a propriedade distributiva, assim como o que foi feito no caso anterior.
(x – a)(x – a) = x2 – ax – xa + a2
Somando os termos semelhantes do resultado, obtemos:
x2 – 2xa + a2
Esse resultado pode ser interpretado da seguinte maneira:
O quadrado do primeiro termo,
menos duas vezes o primeiro, vezes o segundo termo,
somado ao quadrado do segundo termo,
é igual ao quadrado da diferença.
Produto da soma pela diferença
Esse produto notável sempre pode ser escrito na forma de produto entre uma soma e uma diferença, como no exemplo:
(x + a)(x – a)
Aplicando a propriedade distributiva, temos:
(x + a)(x – a) = x2 – xa + ax – a2
Fazendo a adição dos termos semelhantes, obtemos:
x2 – xa + ax – a2 = x2 – a2
Esse resultado pode ser lido da seguinte maneira:
O quadrado do primeiro termo,
menos o quadrado do segundo termo,
é igual ao produto da soma pela diferença
Cubo da soma
O produto notável conhecido como cubo da soma sempre pode ser escrito na seguinte forma:
(x + a)3
Para calcular o resultado do cubo da soma, basta escrevê-lo como produto de três polinômios e usar a propriedade distributiva. Observe:
(x + a)3
(x + a)(x + a)(x + a)
(x + a)(x2 + 2ax + a2)
x3 + 2ax2 + xa2 + ax2 + 2a2x + a3
Feito isso, basta somar os termos semelhantes:
x3 + 2ax2 + xa2 + ax2 + 2a2x + a3
x3 + 3ax2 + 3a2x + a3
Observe que esse resultado pode ser lido da seguinte maneira:
O cubo do primeiro termo,
somado a três vezes o quadrado do primeiro termo, vezes o segundo termo,
somado a três vezes o primeiro termo, vezes o quadrado do segundo termo,
somado ao cubo do segundo termo.
Cubo da diferença
O produto notável conhecido como cubo da diferença é aquele que pode ser escrito da seguinte maneira:
(x – a)3
A solução desse produto notável é dada multiplicando “x – a” por si mesmo três vezes:
(x – a)(x – a)(x – a)
(x – a)(x2 – 2ax + a2)
x3 – 2ax2 + xa2 – ax2 + 2a2x – a3
x3 – 3ax2 + 3a2x – a3
Então, esse resultado pode ser lido da seguinte maneira:
O cubo do primeiro termo,
menos três vezes o quadrado do primeiro termo, vezes o segundo termo,
somado a três vezes o primeiro termo, vezes o quadrado do segundo termo,
menos o cubo do segundo termo.
Aproveite para conferir nossa videoaula sobre o assunto: